After submitting an air cargo optimization solution for the Airbus Quantum Computing Challenge one of the future directions of the team was to map our algorithms to the D-Wave annealer and be able to run real larger problems. Now working in the D-Wave Ocean platform and the possibilities with AWS Braket, Quantum-South has been able to scale up the problem and work a model with a significant number of containers. In this article we share our initial findings.
Quantum annealing is an heuristic algorithm that solves combinatorial optimization problems, and D-Wave Systems Inc. has developed hardware implementation of this algorithm. The paper “Improving solutions by embedding larger subproblems in a D-Wave quantum annealer” discusses optimization problems with Hamiltonians that are similar to the ones we used for the aircraft loading.
The D-Wave 2000Q™ System has up to 2048 qubits and 5600 couplers. To reach this scale, it uses 128,000 Josephson junctions, which makes the D-Wave 2000Q QPU by far the most complex superconducting integrated circuit ever built by 2019 when we worked on the aircraft loading optimization problem for the Airbus Quantum Computing Challenge. In September 2019 D-Wave announced its newest offering to be available in mid-2020, it would offer two and a half times more connectivity between qubits than the 2000Q quantum computer. Announcing their fifth-generation, the 5,000-qubit system named Advantage would be made available for on-premise deployments and in D-Wave’s Leap cloud service in mid-2020 . The Advantage design incorporates D-Wave’s new Pegasus topology , which was announced in February 2019. The new topology design provides higher connectivity, influencing how problems are solved. Higher connectivity allows more complex problems to be solved using the same number of qubits. With higher connectivity, less qubits are needed to solve problems.
D-Wave’s Ocean software development kit includes a suite of open-so0urce Python tools on the D-Wave GitHub repository for solving hard problems with quantum computers. The software stack implements the computations needed to transform an arbitrarily posed problem to a form solvable on a quantum solver .
The D-Wave system uses a quantum processing unit (QPU) to solve a binary quadratic model (BQM): given N variables x1,…,xN, where each variable xi can have binary values 0 or 1, the system finds assignments of values that minimize
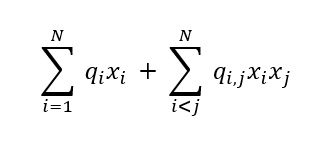
where qi and qi,j are configurable (linear and quadratic) coefficients. To formulate a problem for the D-Wave system we need to program qi and qi,j so that assignments of x1,…,xN also represent solutions to the problem.
The “native” forms of BQM programmed into a D-Wave system are the Ising model traditionally used in statistical mechanics and its computer-science equivalent, the QUBO (Quadratic unconstrained binary optimization).
From quantum algorithms like variational quantum eigensolver (VQE), instead we can use a quantum annealer, e.g. a D-Wave machine for such calculations.
We also have taken a look at the paper “Electronic Structure Calculations and the Ising Machine”.
The Hamiltonian we are using for our problem can be adjusted to match what is shown in D-Wave’s documentation. Basically, when everything is multiplied out from the image Hamiltonian, we end up with constants, linear terms, and quadratic terms. Because we are searching for an ArgMin of the objective function rather than the min (finding where the minimum value occurs rather than the minimum value itself), we can ignore constant terms. This will leave us with linear and quadratic terms only, matching what we have in D-Wave’s documentation.
While we likely will be able to run larger problems on D-Wave’s system than on the IBM one, it is important to have in mind that the embedding step of a Hamiltonian uses far more qubits than logical variables in the optimization function. Because the chip does not have all-to-all connectivity between qubits, we had to do further analysis on our Ising model, and we would be able to run an Ising model with at least 64 logical variables.
Working on September 2019, with the 6 connections from each physical qubit, D-Wave could create up to 64 fully connected logical qubits using the 2000 qubits available and hence the last point. Obviously, in a situation where variables are less dependent upon each other (and need fewer interconnections), we can manage problems with a greater number of variables. In addition, D-Wave has a number of software tools to allow us to accommodate much larger numbers of variables.
By October 2019 we had the expectation of being able to map our algorithms in D-Wave annealer in the short term and be able to run real larger problems. The restriction we had with IBM/Google of the order of 50 qubits, by moving to D-Wave would exceed 100 and reach more than 1000, which would be a significant amount of containers in our problem.
We created an account on D-Wave to use the leap service, which is an on-line IDE that has already installed all the necessary libraries for development using Python. It is an easy-to-use interface, even for people that does not have much experience using advanced tools for coding.
As mentioned, the problems on the quantum computers fabricated by D-Wave are solved with Quantum Annealing, and the problems are submitted under the form of binary quadratic models. We did a good research about all these concepts.
When programming the algorithms we followed the form of the classical Quadratic Knapsack Problem (QKP): given a set of packets to transport and a bag, with price and weight associated to each packet, the objective is to maximize price with a maximal weight allowed to carry on the bag. This was a first approach for solving the real problem, then more constraints where added such as the size of each container. Also, the classical formulation of the QKP had to be adapted to a BQM. Here there are two ways to do it: As an Ising model, or a quadratic unconstrained binary optimization (QUBO) model. In our case we chose the second approach.
Finally, we escalated our problem, it had the capability of managing around 50 different containers with different sizes and weights. Bear in mind that the containers are units that have multiple packages inside, so, these numbers are quite good.
For the future we expect to reach bigger numbers and add more constraints so we can expand our algorithm to more than just planes. Today quantum computers are still being developed and their growth and accuracy will be better over the next years. Along with that, some pre-processing of the data is being researched to make our solution more performant.
